University

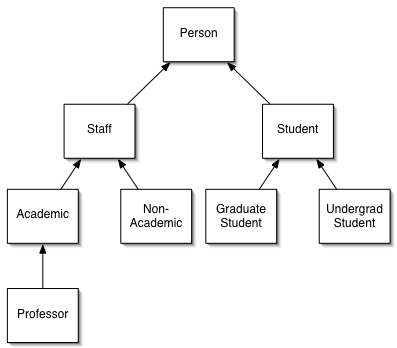
This example is based on a simple model of a University department.

Basic Classes

The department consists of Staff who can be Academic staff or Non-Academic Staff, Professors and Students. Professors are Academic Staff, Students can be Graduate Students or Undergraduate Students. The situation is summarised in the diagram below.

Person Hierarchy

The department offers a number of Modules in Mathematics, Computer Science or Economics (no module can be in two areas). Each module is taught by a single academic. We have chosen to model this as subclasses ComputerScienceModule, EconomicsModule and MathematicsModule.

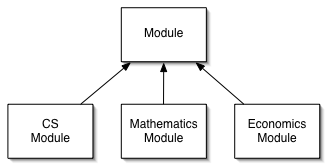
Person Hierarchy

Each Undergraduate Student takes a number of modules (for the purposes of this model, we assume that Graduate Students are involved purely in research projects, thus the only students that take course are UndergraduateStudents).

Basic Facts

The tables below show some known facts that populate the model.

Module Area Teacher
CS101 Computer Science Prof1
CS102 Computer Science Prof2
CS103 Computer Science Prof3
CS104 Computer Science Prof1
CS105 Computer Science Prof3
MT101 Maths Prof4
MT102 Maths Prof5
MT103 Maths Prof6
EC101 Economics Prof4
EC102 Economics Prof7
EC103 Economics Prof1
Student Modules
Student1 CS101 CS102
Student2 CS101 MT101
Student3 MT101 EC103
Student4 CS101 MT101
Student5 MT102 MT103

Honours Students

The example ontology university1 defines the classes above.

A Joint Honors Maths & Computer Science Student is one who takes both Computer Science and Mathematics modules. A Single Honours Maths [Computer Science, Economics] Student is one who takes only Maths [Computer Science, Economics] modules.

One way of trying to define a Joint Honours Maths/CS Student would as below:

Class(JointHonoursMathsCSStudent complete intersectionOf(student
  restriction(takes someValuesFrom (
    intersectionOf( MathsModule ComputerScienceModule ) ) ) ) )

This is "wrong", however, as it's saying that a Joint Honours Student is one who takes something that is both a MathsModule and a ComputerScienceModule. This is impossible as the two classes are disjoint. This definition is thus inconsistent — it is impossible for there ever to be any instances of this class.

Rather, we should define it as:

Class(JointHonoursMathsCSStudent complete intersectionOf(student
  restriction(takes someValuesFrom ( MathsModule ) )
  restriction(takes someValuesFrom ( ComputerScienceModule ) ) ) )

This then states that a Joint Honours Maths & Computer Science Student is one who takes a MathsModule and takes a ComputerScienceModule.

For the Single Honours Maths Student, we could define 

Class(SingleHonoursMathsStudent complete intersectionOf(student
  restriction(takes allValuesFrom ( MathsModule ) ) ) )

This captures the fact that all modules taken must be MathsModules. However, you will see that those students that only take MathsModules don't appear under this definition. The issue here is again the Open World Assumption -- we don't know that these students don't take any other modules.

Note also that this definition will subsume GraduateStudent. The domain of takes is UndergraduateStudent and this is disjoint from GraduateStudent. Thus we know that no GraduateStudent can take any Modules, so all Modules they take are MathsModules. Again an example of universal quantification over an empty set.

In this particular case, we cannot effectively capture the notion of a generic Single Honours student. One solution would be to define a Single Honours Maths Student as above and a Single Honours Computer Science Student similarly, then define the generic Single Honours as the union of the two. The problem then is that if we introduce a new subject area, we need to then rework this definition. This is an example of a situation where OWL's expressivity is not enough to capture what we want to say. The situation is the same with Joint Honours. OWL does not give us sufficient expressivity to capture the class of individuals that take modules that are from different classes (without explicitly stating what those classes are).

The table below shows some additional information about more students. Where the module code contains question marks, we have some partial information. So we know that Student 6 takes two modules, but we don't know the second one. Student 7 takes some unknown CS module.

Student Modules
Student6 MT101 ?????
Student7 CS101 MT???
Student8 CS102 EC???

Example ontology university2 encodes the information about the students listed above.

You should be able to infer that Student7 is a Joint Honours Student. Even though we don't know the module that Student7 takes, we know it is a Maths module.

Restricting Modules

The university has a regulation that each undergraduate student must take exactly 2 modules.

We can use a cardinality restriction as follows:

Class( Student partial ( takes maxCardinality( 2 ) ) )

This states that a student can take at most 2 classes. Note that in this case, the original definition of a Single Honours Maths Student will then include those students that only take MathsModules. The cardinality constraint allows us to infer that the two modules named must be the only modules that the student takes.

Student Modules
Student9 MT101 CS101 CS102

Example university3 includes the restriction identified above and a definition of Student9.

Student Modules
Student10 MT101 CS101 EC101

Example university4 includes a definition of Student10.

What should happen here is that the reasoner is happy with student9, but complains once we introduce student10. Even though student9 takes three modules, there is nothing in the model that says that CS101 and CS102 must be different objects. Thus an acceptable situation is that CS101 and CS102 refer to the same object, and thus student9 does indeed take two modules.

For student10, however, the disjointness of the various modules means that the three course named must be different, thus we have an inconsistency. Note also that the way that the reasoner reports the inconsistency may not talk about student10.

Again, here we must be explicit about the things that are different. OWL does not make the Unique Name Assumption, so we must say which individuals we expect to be distinct. Adding an axiom asserting that all the courses are different objects would then cause the reasoner to spot the "error" in the information about student9.

Extensions

If you have time remaining at the end of the session, consider extending the model to cover Teaching Assistants. Teaching Assistants are Graduate Students that are also Non-Academic staff who assist with teaching on particular modules. Each module may have at most one TA associated with it. Alternatively, use the information about members of staff in order to define classes such as Professors who only teach on, say, Mathematics courses.